Uncertainty Quantification
Quantifying uncertainty is a key capability for (semi)autonomous systems, in order to understand when the model is uncertain, e.g., when it encounters something unknown (out of distribution, OOD). For instance, robot SPOT is in a place that it does not know, so it can invoke assistance or go in safe mode.
Our experiment is illustrated below: three categories of places are known (Home, Work, Public places), and, one category is unknown: Shops (seen only at test time).

We have researched prototypes for this purpose. The paper is published at a NeurIPS workshop about uncertainty.
Prototypes are a set of vector representations, one for each class. We propose equidistant hyperspherical prototypes that are maximally separated, such that OOD samples fall in between. We show that in practice this indeed happens. The distance to such a prototype is a good quantification of uncertainty.
The figure shows an example of 4 classes and their prototype in 3D, with learned projections of samples (dots) and the samples that are considered to be outliers (squares).
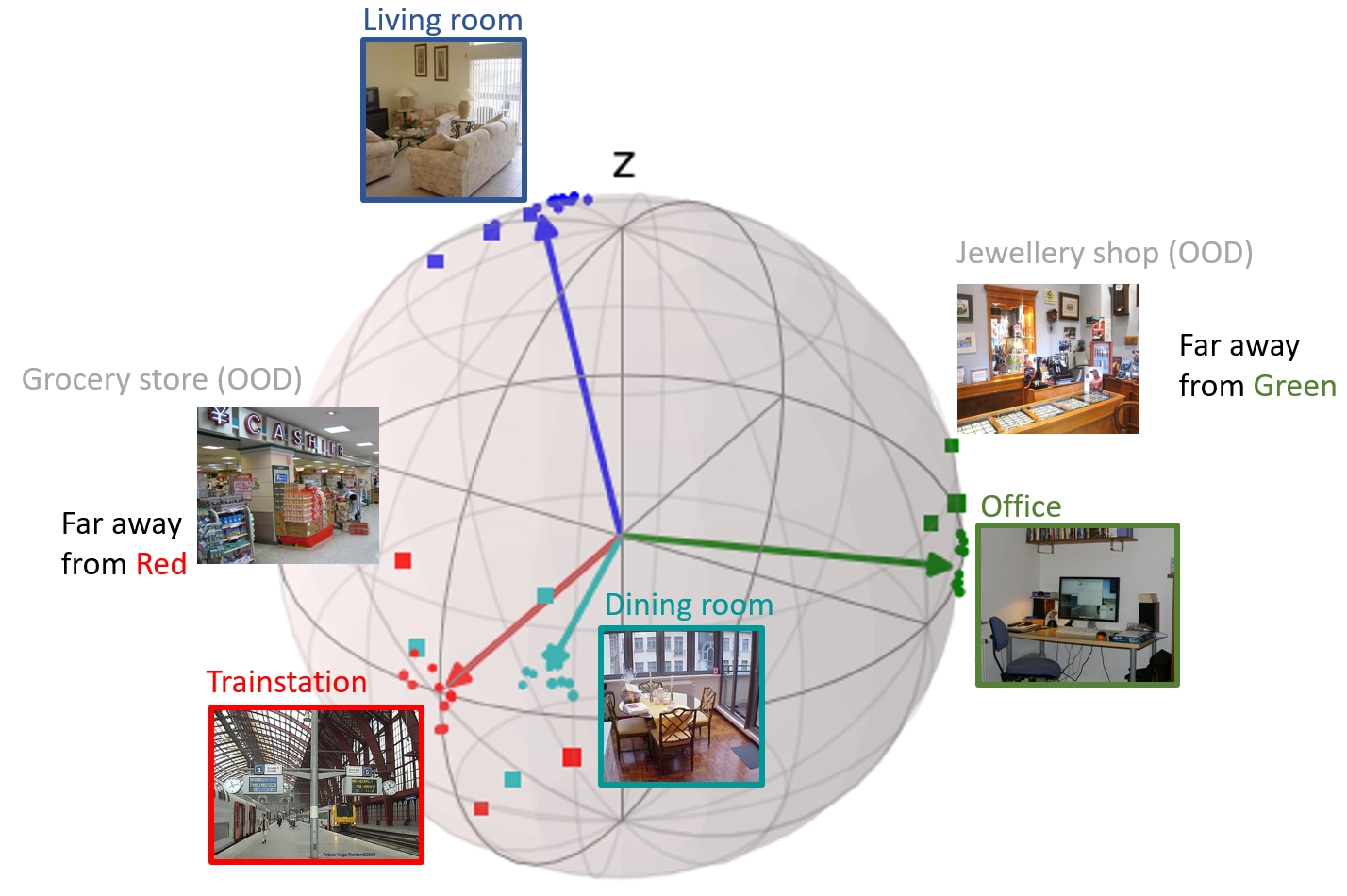
For a robot, it is important that it understands in what kind of environment it is, and how certain it is about that. Therefore, we experimented with the MIT Indoor Places dataset. Three categories are learned (Home, Work, Public places) and one category is unknown (Shops).
We show that the approach is able to quantify higher uncertainties for the unknown samples (AUC=0.88). It performs very favorably over conventional onehot + softmax, which is often over-confident about the unknowns (AUC=0.61).
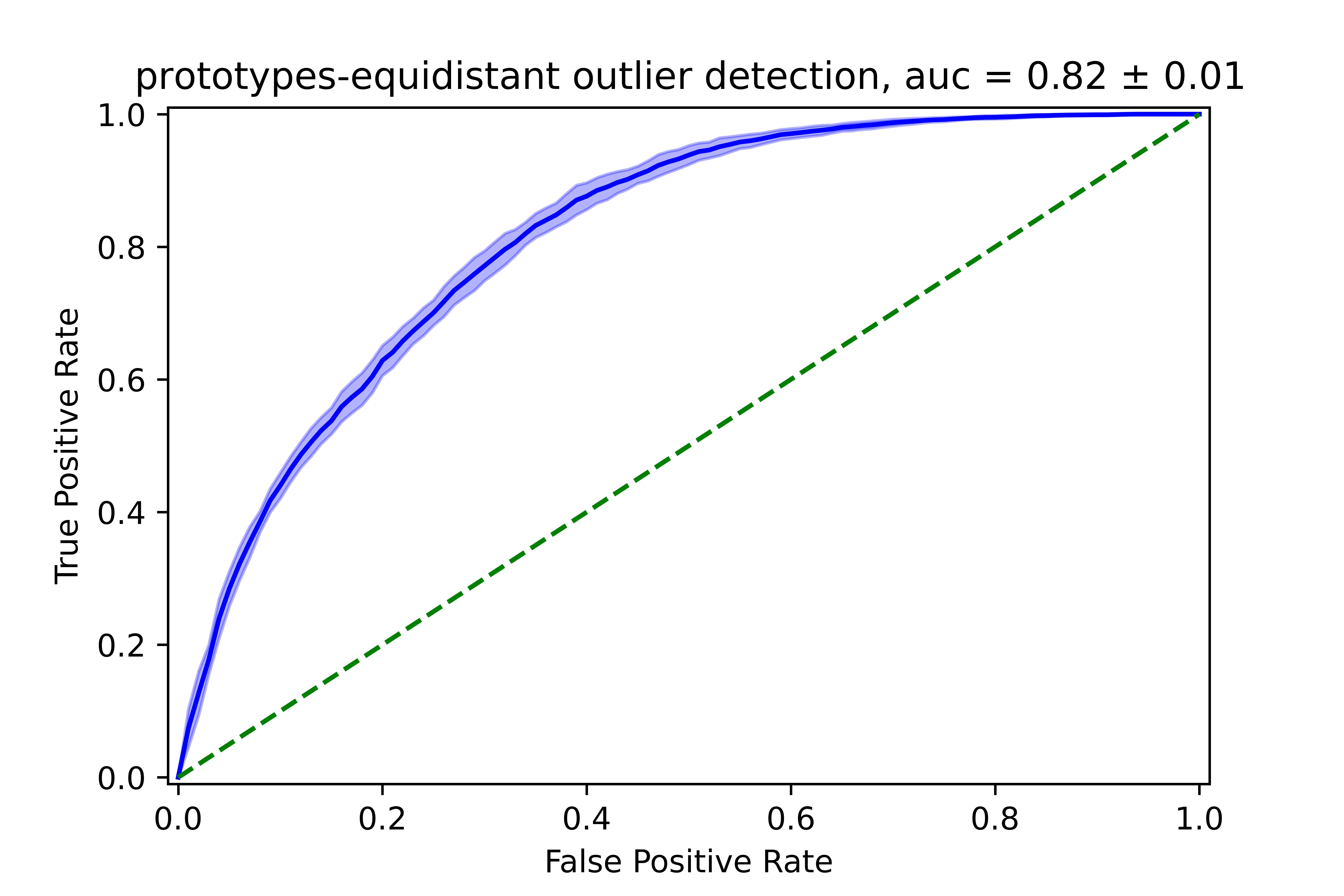
This research is part of Appl.AI SNOW (Context Awareness).